Introduction
The adaptive radix tree is a variant of the radix tree that has adaptive node sizes.
Adaptive node sizes give space-efficiency because all nodes do not need to be the same size. For instance, consider needing to support 256 children in each node, and the case where the majority of nodes have fewer than 16 children.
For more information, refer to “The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases” by Viktor Leis.
Features
Some properties of note for a radix tree:
- the tree’s height depends on the length of the keys instead of the number of elements.
- the tree does not require re-balancing.
- the tree’s layout is unaffected by insertion order.
- the tree’s keys stored in order.
- the tree’s keys can be translated to a path from the root to the leaf node.
- the tree’s height can be reduced by ‘path compression’ and ‘lazy expansion’.
Lazy Expansion & Path Compression
Two techniques for reducing the height of the tree and, space consumption.
Lazy expansion
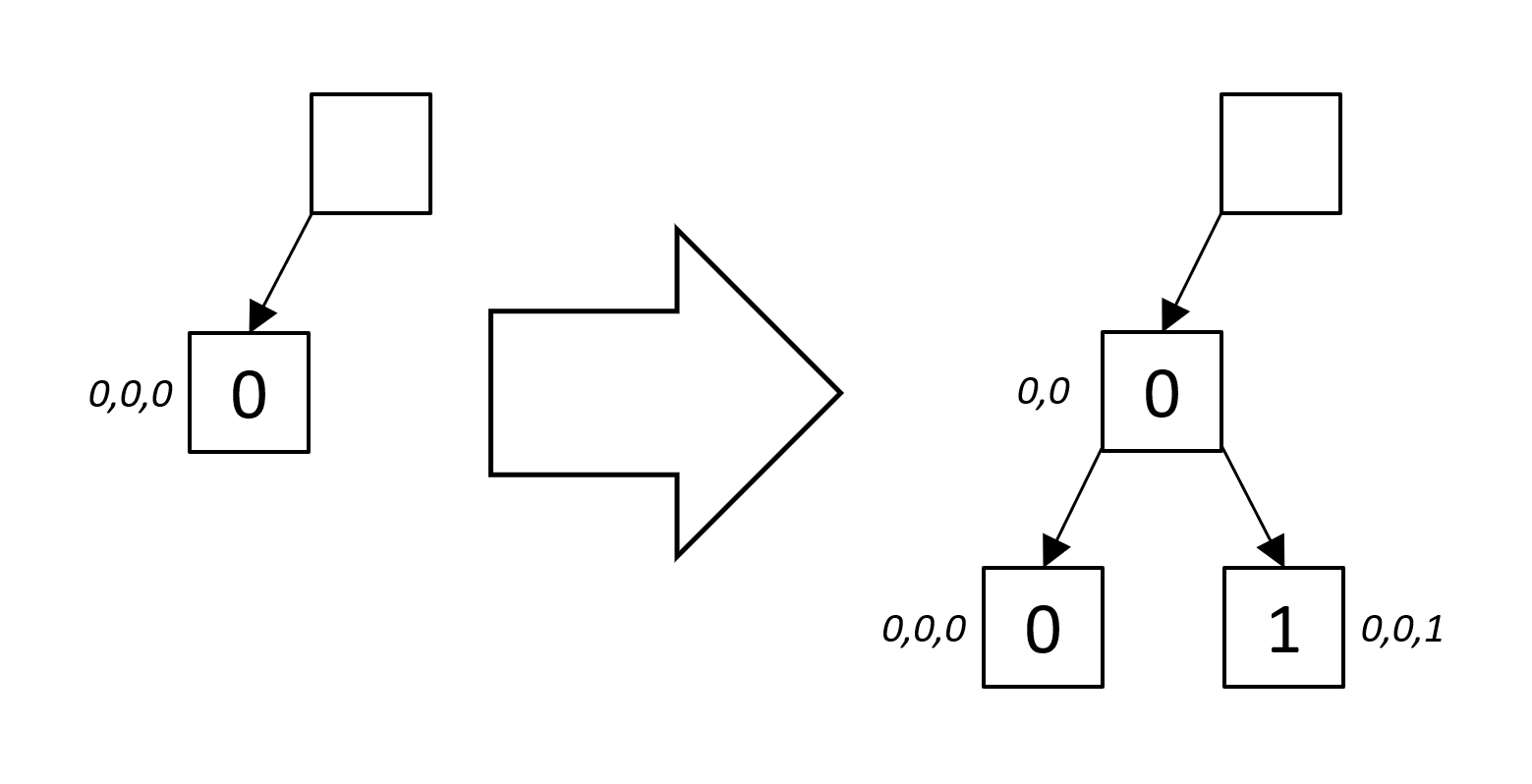
Nodes only created when two nodes need to be distinguished. For instance, when inserting the first value into an adaptive radix tree, only one node needs to be created. Therefore, create intermediate-parent nodes only when creating a branch in the path from the root node to the leaf node.
Path compression
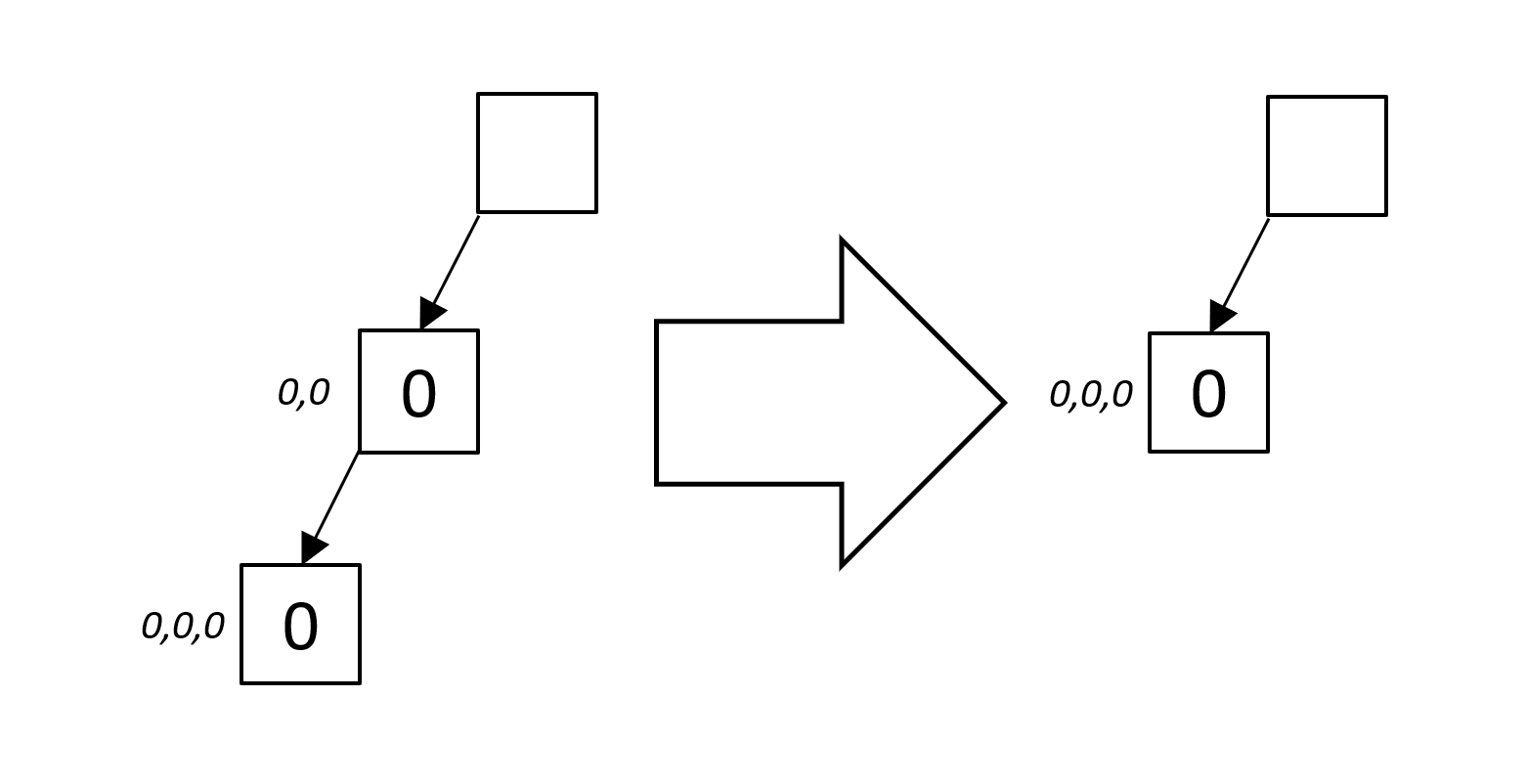
Remove nodes that have only one child. By removing the node, the radix tree integrates/flattens the parent into the child node.
Adaptive Nodes
Each node in the tree can be one of four types.
ArtNode4
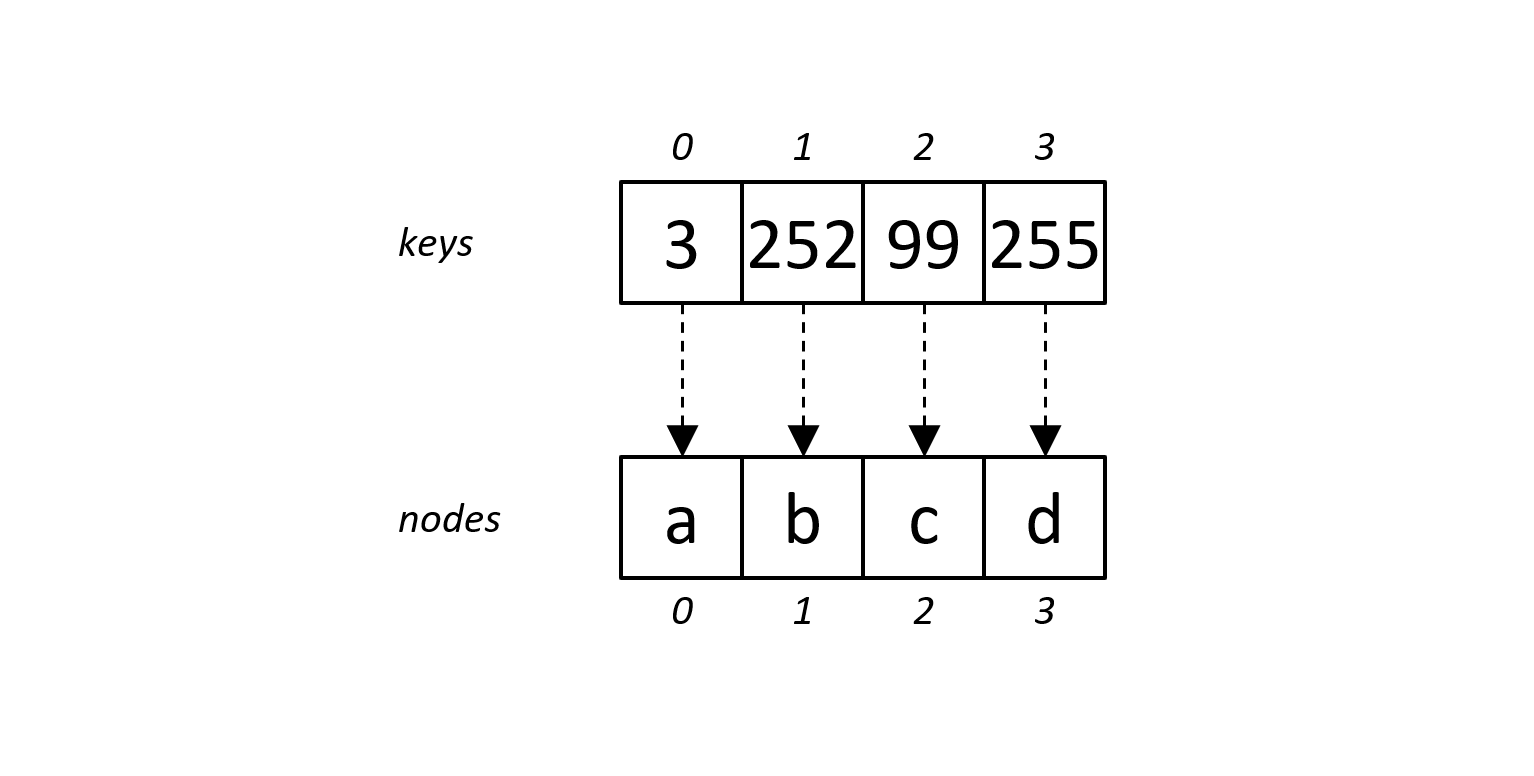
The basic node type can store up to 4 keys and 4 pointers, in two arrays: a key array, and a pointer array. The position (index) in the two arrays line up the key and pointer values.
ArtNode16
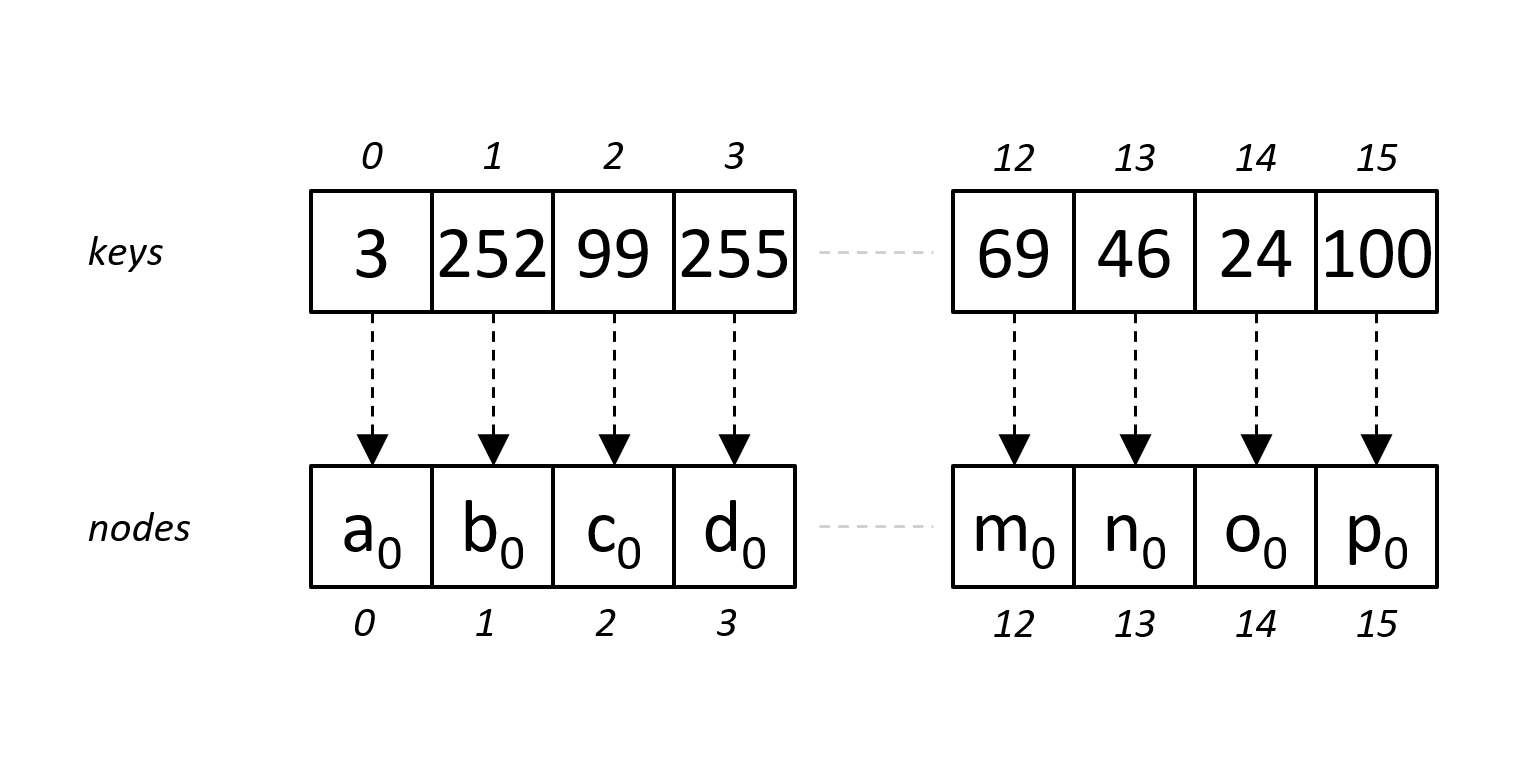
The second node type stores between 5 and 16 keys, and between 5 and 16 pointers. Again, they are stored in two arrays: a key array, and a pointer array. The position (index) in the two arrays line up between the key and pointer values. The keys can be sorted or unsorted in this node type, in my implementation this node type was unsorted while still being performant.
ArtNode48
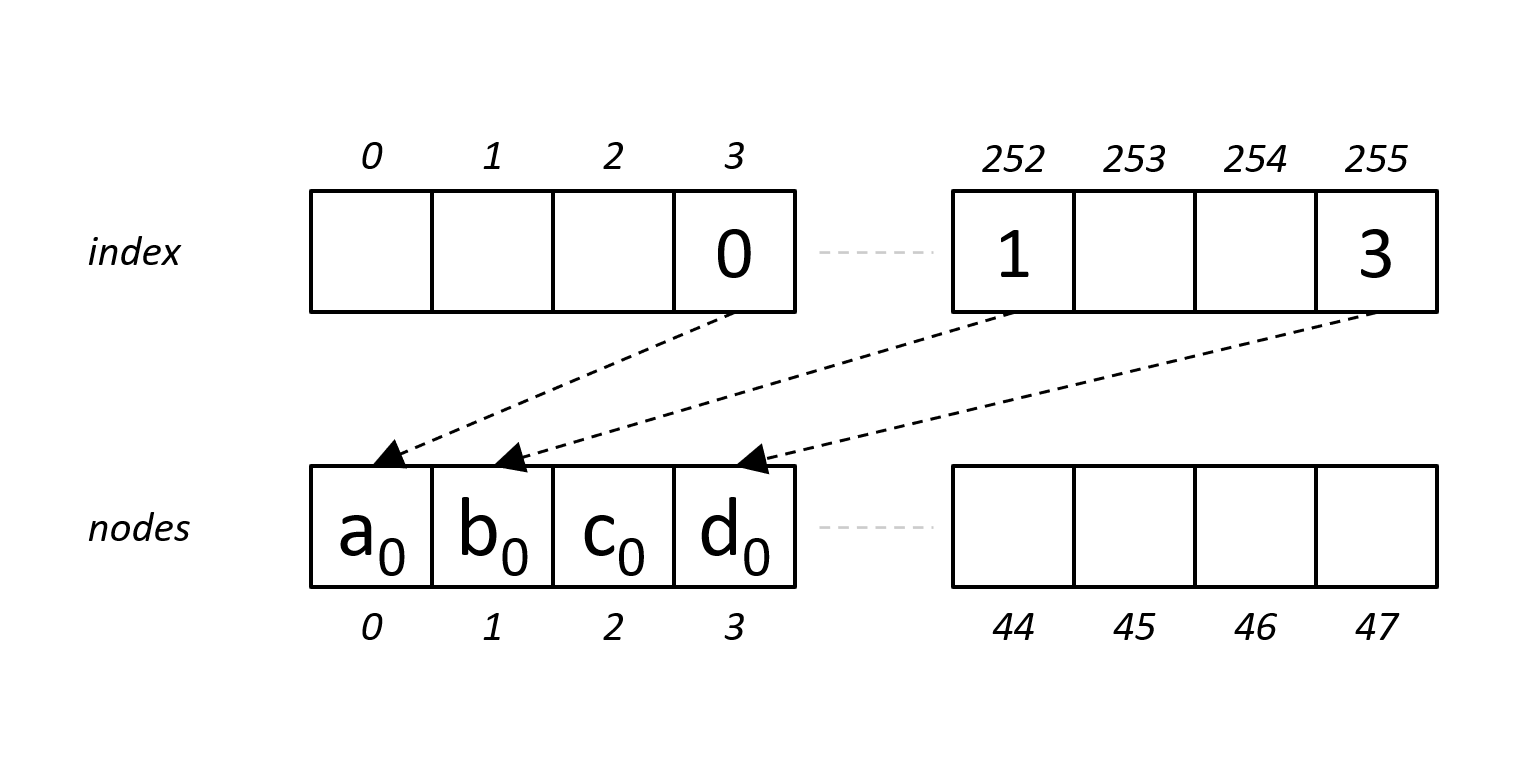
The third node type stores between 17 and 48 keys, and between 17 and 48 pointers. The keys are in an 256-element index array, i.e. the index position identifies the key value and value stored identifies the node index. The pointers are in a 48-element node array.
ArtNode256
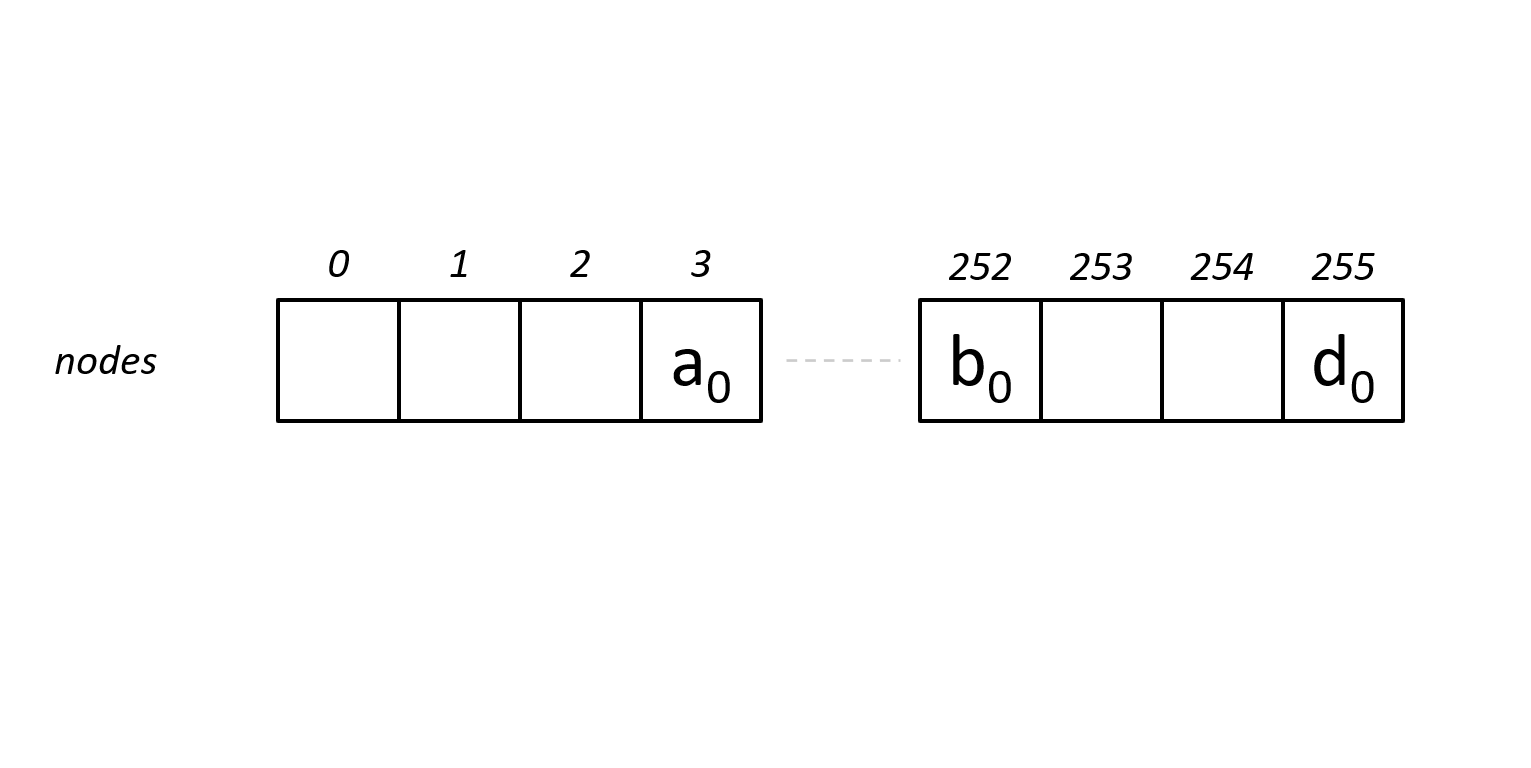
The fourth node type stores between 49 and 256 keys, and between 49 and 256 pointers. A single 256-element array stores the pointers, where the index represents the key value.
As the number of children grows and shrinks, switch to the node the fits the number of children.
Next
In the next post, let’s run through the initial adaptive radix tree implementation.